分布式缓存

2021-12-30 约 2572 字预计阅读 6 分钟

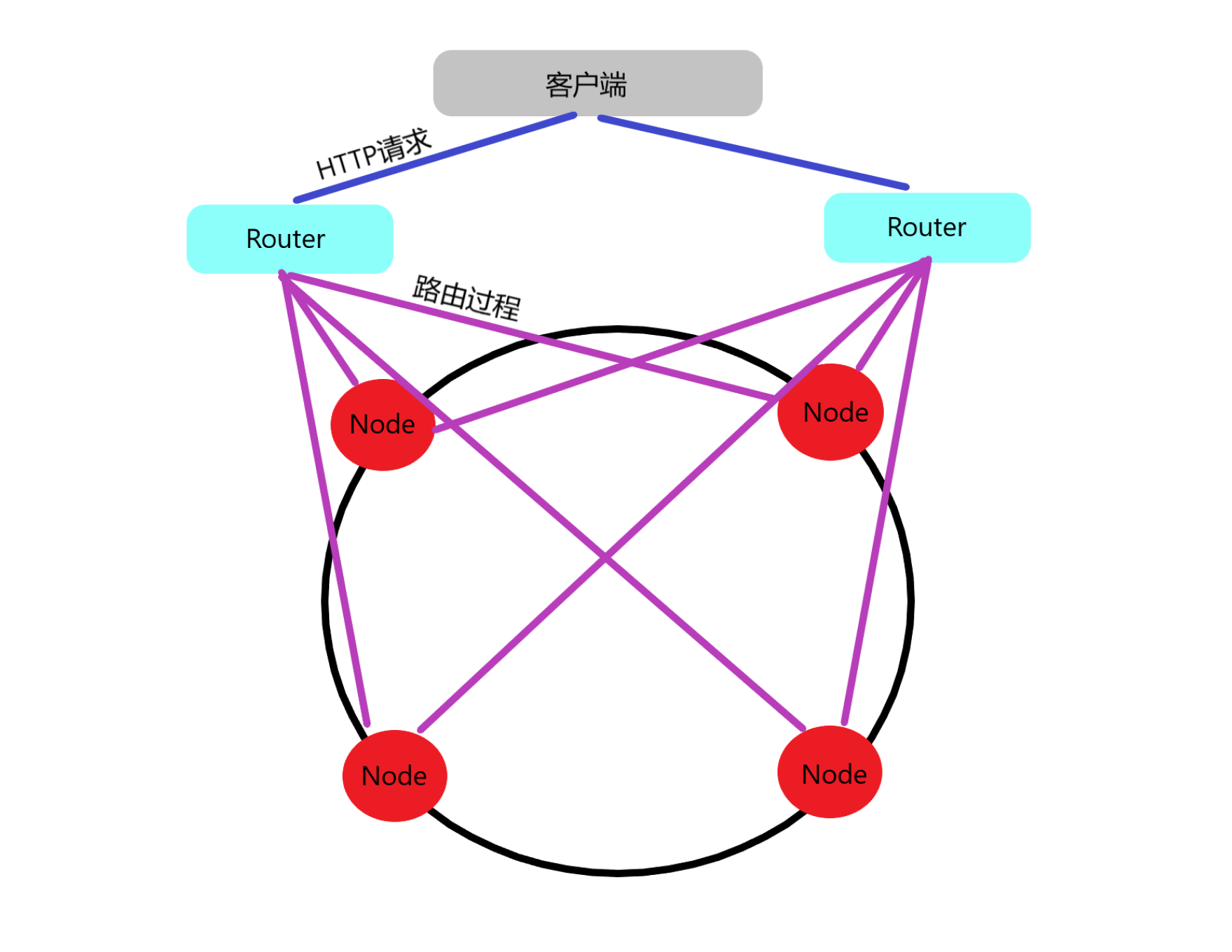
概述

基本信息

项目地址：https://github.com/taofengliu/cache

这是一个纯内存的缓存玩具工具，节点用来存储具体数据，Router用来接受客户请求并路由到对应节点去查询数据。节点内部用LRU算法来管理数据，Router通过一致性哈希算法管理各个节点。Router启动时会对节点进行简单的测试，确认节点地址正确。Router有感知节点宕机的功能，当查询或设值的节点已经无法使用，Router会删除该节点。在设值时会自动反复重新尝试设值，若所有节点均失效，则Router关闭。

项目的设计灵感来源于《数据密集型应用系统设计》第203页的方案2。

启动方法

启动一个节点： run go run_nodeserver.go -端口号 -LRU容量(单位：字节)

启动一个Router： run go run_router.go 多个节点地址（以空格分隔） -端口号 -每个真实节点对应的虚拟节点数

HTTP API

GET {Router地址}/cache/{key值} 来进行查询

POST {Router地址}/cache/{key值} 来进行设值，值通过http body发送

DELETE {Router地址}/cache/{key值} 来进行删值

LRU算法

双向队列

双向队列就是真正存储每个LRU元素的地方，它有长度限制，如果达到长度上限，那么再添加元素时队列末端的元素就会被挤出队列，每当插入或查询一个元素，它总会被放到队首。

首先定义队列节点。

1
2
3
4
5
6
7


// Element 队列节点，包含Data用来存储数据
type Element struct {
	Key   string
	Value Data
	Pre   *Element
	Next  *Element
}

再来定义一个双向队列，它包含一个头节点和尾节点。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


// LinkedList 一个双向队列
type LinkedList struct {
	Head *Element
	Tail *Element
}

//初始化方法，空的双向队列首尾节点相连
func New() *LinkedList {
	head := Element{
		Key:   "Head",
		Value: Data{},
	}
	tail := Element{
		Key:   "Tail",
		Value: Data{},
	}
	head.Next = &tail
	tail.Pre = &head
	list := LinkedList{
		Head: &head,
		Tail: &tail,
	}
	return &list
}

为了方便删除元素、将元素添加到队首，再来写两个方法。这时候双向队列就已经写完了，接下来就是要用它和HashMap组合完成一个LRU算法了。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


// Remove 删除一个元素
func (list *LinkedList) Remove(element *Element) {
	next := element.Next
	pre := element.Pre
	next.Pre = pre
	pre.Next = next
}

// AddToHead 将一个元素加到队列头部
func (list *LinkedList) AddToHead(element *Element) {
	head := list.Head
	headNext := head.Next
	head.Next = element
	headNext.Pre = element
	element.Next = headNext
	element.Pre = head
}

双向队列与HashMap组合实现LRU

首先定义一个Cache结构，包含最大容量值、当前容量值、一个双向队列和一个HashMap，HashMap的作用是通过key值在O(1)复杂度内获得对应的队列元素，我还添加了一个回调函数用于测试。

1
2
3
4
5
6
7


type Cache struct {
	maxCapacity int //最大容量
	capacity    int //当前容量
	list        *linkedlist.LinkedList
	cache       map[string]*linkedlist.Element
	OnEvicted   func(key string, value linkedlist.Data) //当一个element被删除时执行该方法
}

之后便是最重要的Get和Add方法。Get方法的实现思路就是根据key在HashMap中获得对应的队列元素，将元素移动到队首，然后返回元素中的数据。Add方法可以先调用Get方法判断该key值是否已经存在于队列中，如果已存在，Get方法已经将对应元素移至队首，只需更改对应的元素中的数据；如果不存在，则新建元素并加至队首。添加成功之后，还要判断LRU容量是否超出预设的最大值，若超出最大值，需要删除队尾元素直到容量小于等于预设的最大值。至此，LRU算法就已经完成。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40


func (c *Cache) Get(key string) (value linkedlist.Data, ok bool) {
	if element, ok := c.cache[key]; ok {
		list := c.list

		//删除element再将其加到队列头部
		list.Remove(element)
		list.AddToHead(element)

		return element.Value, true
	}
	return linkedlist.Data{}, false
}

func (c *Cache) Add(key string, value linkedlist.Data) {
	if _, ok := c.Get(key); ok {
		c.cache[key].Value = value
	} else {
		element := linkedlist.Element{
			Key:   key,
			Value: value,
		}
		c.list.AddToHead(&element)
		c.cache[key] = &element
		c.capacity += element.Value.Length()

		//容量超过限度
		for c.capacity > c.maxCapacity {
			toRemove := c.list.Tail.Pre
			c.list.Remove(toRemove)
			delete(c.cache, toRemove.Key)
			c.capacity -= toRemove.Value.Length()

			//执行回调方法
			if c.OnEvicted != nil {
				c.OnEvicted(toRemove.Key, toRemove.Value)
			}

		}
	}
}

一致性哈希算法

多种方案

方案一：数组+排序

算出所有待加入的节点的Hash值放入一个数组中，然后使用排序算法将其从小到大进行排序。路由一个key时，算出其Hash值，只需要在数组中找到第一个Hash值比它大的节点就可以了。比如服务器节点的Hash值是 [0,2,4,6,8,10]，待路由的节点的Hash值是7，则只需要找到第一个比7大的整数，也就是8，就是我们要找的最终需要路由过去的服务器节点。

这种方案下，增删一个节点的时间复杂度为O(nlogn)，路由的复杂度为二分查找的O(logn)。这里要注意如果在线添加节点，因原数组已经有序，在加入一个元素后使用传统的快速排序效率很低。

方案二：遍历+List

由于排序比较消耗性能，那么可以选择不排序，采用直接遍历的方式。服务器节点的Hash值不排序，全部放到一个List中。当路由一个key时，算出其Hash值，遍历List，比待路由节点 Hash值大的算出差值并记录，比待路由节点Hash值小的忽略，算出所有的差值之后，最小的那个，就是最终需要路由过去的节点。

这种方案下，增删一个节点的时间复杂度为O(1)，路由的复杂度为O(n)。

方案三：红黑树

红黑树主要的作用是用于存储有序的数据，因此相当于省略了排序这步骤。在这个方案下，增删和查找的时间复杂度均为O(logn)。

具体实现

我选择的是带有虚拟节点的方案一，因为它最简单(狗头)。

首先定义一个Map结构，它就可以代表一个哈希环了。

1
2
3
4
5
6


type Map struct {
	hash     Hash           //Hash函数，我默认使用的是CRC32
	replicas int            //虚拟节点的倍数，代表每个真实节点对应几个虚拟节点
	Keys     []int          //经过排序，存储所有节点的哈希值
	hashMap  map[int]string //虚拟节点和真实节点的映射，虚拟节点即为一个hash值，真实节点为一个地址
}

接下来的Get、Delete和Add方法均与上面方案一的描述相符，具体见代码与注释。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


// Add 向Map中添加真实节点
func (m *Map) Add(addrs ...string) {
	for _, addr := range addrs {

		//添加虚拟节点
		for i := 0; i < m.replicas; i++ {
			hash := int(m.hash([]byte(strconv.Itoa(i) + addr)))

			//将节点的哈希值加入切片
			m.Keys = append(m.Keys, hash)

			//将虚拟节点映射到真实节点地址
			m.hashMap[hash] = addr
		}

	}
	sort.Ints(m.Keys) //使数组有序
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


// Delete 从Map中删除元素
func (m *Map) Delete(addrs ...string) {
	for _, addr := range addrs {

		//删除虚拟节点
		for i := 0; i < m.replicas; i++ {
			hash := int(m.hash([]byte(strconv.Itoa(i) + addr)))

			//从切片中删除虚拟节点的哈希值
			index := sort.SearchInts(m.Keys, hash)
			m.Keys = append(m.Keys[:index], m.Keys[index+1:]...)

			//删除map中的映射
			delete(m.hashMap, hash)

		}

	}
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


// Get 根据key值来确定真实节点地址
func (m *Map) Get(key string) string {
	if len(m.Keys) == 0 {
		return ""
	}
	hash := int(m.hash([]byte(key)))

	//二分查找大于key的哈希值的最小虚拟节点哈希值
	idx := sort.Search(len(m.Keys), func(i int) bool {
		return m.Keys[i] >= hash
	})

	//取模是因为key的hash可能大于所有节点的hash，这时应定位到第一个节点
	return m.hashMap[m.Keys[idx%len(m.Keys)]]
}

目录